Problème des ménages

Une table à dix couverts. D'après la solution au problème des ménages, il y a 3 120 manières différentes, pour 5 couples, de s'asseoir en alternant hommes et femmes et sans qu'aucun convive soit assis à côté de son (ou sa) conjoint(e).

En mathématiques combinatoires, le problème des ménages est la question du nombre de façons différentes de placer un nombre donné de couples hétérosexuels monogames autour d'une table de façon à alterner hommes et femmes et à ne placer personne à côté de son (ou sa) conjoint(e). Ce problème fut formulé en 1891 par Édouard Lucas et indépendamment, quelques années plus tôt, par Peter Guthrie Tait, en relation avec la théorie des nœuds. Pour un nombre de couples égal à 3, 4, 5, ... le nombre de placements possibles est

12, 96, 3120, … (suite A059375 de l'OEIS).

Des formules et des relations de récurrence permettent de calculer cette suite d'entiers ainsi que d'autres suites liées à ce problème. Au-delà de leurs applications aux plans de table, ces nombres interviennent en théorie des nœuds et ont une interprétation en théorie des graphes : ce sont les nombres de couplages et de cycles hamiltoniens dans certaines familles de graphes.

Formule de Touchard

Jacques Touchard a donné en 1934 la première formule explicite pour le nombre M_n de façons de disposer n couples :

$M_{n}=2(n!)\sum _{k=0}^{n}(-1)^{k}{\frac {2n}{2n-k}}{2n-k \choose k}(n-k)!$ .

À sa suite, de nombreux mathématiciens ont fourni diverses preuves de cette formule et des versions généralisées du problème, où l'on autorise certains conjoints à être côte à côte. Wyman et Moser, en 1958, ont découvert pour M_n une autre formule, qui met en jeu les polynômes de Tchebychev.

Nombres de ménages et solutions « les dames d'abord »

Les premières solutions au problème des ménages consistaient à placer d'abord les femmes puis à compter, pour chacun de ces placements partiels, le nombre de façon de placer les hommes sans qu'aucun soit à côté de son épouse. Cependant, en 1986, Bogart et Doyle ont donné une preuve plus directe de la formule de Touchard.

Il y a 2(n !) façons de placer les femmes, puisqu'il y a deux choix possibles pour l'ensemble des sièges destinés aux femmes et, pour chacun des deux, n! façons de répartir les femmes sur ces n sièges. Pour chacun de ces 2(n !) placements des femmes, le nombre de façons de placer les hommes est

$A_{n}=\sum _{k=0}^{n}(-1)^{k}{\frac {2n}{2n-k}}{2n-k \choose k}(n-k)!$ ;

c'est la même formule que celle de Touchard, au facteur 2(n !) près. La suite A000179 de l'OEIS de ces entiers plus petits, appelés nombres de ménages commence par

A₃ = 1, A₄ = 2, A₅ = 13, …

Ils satisfont la relation de récurrence

$A_{n}=nA_{n-1}+{\frac {n}{n-2}}A_{n-2}+{\frac {4(-1)^{n-1}}{n-2}}$

et la récurrence d'ordre 4 plus simple

$\displaystyle A_{n}=nA_{n-1}+2A_{n-2}-(n-4)A_{n-3}-A_{n-4}$ ,

qui permettent de les calculer facilement. (Des relations de récurrence plus compliquées ont été décrites auparavant par Cayley et Muir.)

Interprétation en théorie des graphes

Graphes couronnes à 6, 8, et 10 sommets. Le cycle extérieur de chaque graphe forme un cycle hamiltonien, mais les graphes à 8 et 10 sommets en possèdent d'autres.

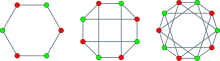
Les solutions du problème des ménages peuvent s'interpréter en termes de théorie des graphes, comme les cycles hamiltoniens orientés de graphes couronnes. Un graphe couronne s'obtient en supprimant un couplage parfait dans un graphe biparti complet K_n,n ; il a 2n sommets, dont n d'une couleur et n d'une autre, et chaque sommet d'une couleur est relié (par une arête) à tous les sommets sauf un de l'autre couleur. Dans le cas du problème des ménages, les sommets du graphe représentent les hommes et les femmes, et les arêtes représentent les paires constituées d'un homme et d'une femme autorisés à s'asseoir côte à côte. Ce graphe est formé à partir du graphe biparti complet qui connecte chaque homme à chaque femme, en supprimant le couplage parfait des arêtes joignant chaque homme à son épouse. À tout placement valide correspond un ordre des convives autour de la table, qui forme un cycle hamiltonien du graphe. Mais deux placements peuvent donner le même ordre circulaire (en) donc le même cycle hamiltonien, s'ils ne diffèrent que d'un décalage autour de la table. Par conséquent, le nombre de cycles hamiltoniens orientés du graphe couronne est égal au quotient par 2n du nombre de placements possibles, donc au produit par (n − 1)! du nombre de ménages A_n.

La suite A094047 de l'OEIS de ces nombres de cycles dans ces graphes (en débutant, comme dans les deux suites précédentes, à n = 3) commence par

2, 12, 312, …

Il existe une deuxième description de ce problème en termes de théorie des graphes. Une fois les femmes assises, les placements possibles pour les hommes correspondent aux couplages parfaits d'un graphe obtenu à partir d'un graphe biparti complet en supprimant un cycle hamiltonien : le graphe biparti complet est constitué des hommes et des chaises libres, et on enlève les arêtes joignant chaque homme aux deux chaises qui sont de part et d'autre de son épouse. Le problème de compter les couplages dans un graphe biparti, et a fortiori celui de calculer les nombres de ménages, peut se résoudre en faisant intervenir les permanents de certaines matrices constituées de 0 et de 1. Dans le cas du problème des ménages, ce sont des matrices circulantes.

Théorie des nœuds

La motivation de Tait pour étudier le problème des ménages est venue de sa recherche d'une liste complète des nœuds ayant un nombre de croisements (en) donné. Dans la notation de Dowker pour les diagrammes de nœuds, dont une forme initiale a été utilisée par Tait, les 2n points des n croisements d'un nœud sont numérotés de 1 à 2n en suivant l'ordre de parcours sur le brin. Dans un diagramme réduit, les deux numéros correspondant à un croisement ne peuvent pas être consécutifs, donc l'ensemble des n paires de numéros correspondant aux n croisements, qui est utilisé dans cette notation de Dowker pour représenter le nœud, peut s'interpréter comme un couplage parfait dans un graphe : les sommets sont les nombres de 1 à 2n et deux sommets sont reliés par une arête lorsqu'ils sont de parités différentes et ne sont pas consécutifs (modulo 2n). Comme ce graphe s'obtient à partir d'un graphe biparti complet (reliant toutes les paires de nombres de parités différentes) en supprimant un cycle hamiltonien (les arêtes reliant des nombres consécutifs), son nombre de couplages est égal à un nombre de ménages. Si le nœud est alterné, ce couplage suffit à décrire son diagramme ; sinon, on spécifie en plus, pour chaque croisement, un signe + ou - pour déterminer lequel des deux brins passe par-dessus l'autre.

Cependant, le problème de Tait comporte des symétries supplémentaires qui sont absentes du problème des ménages : deux notations de Dowker peuvent représenter le même diagramme, donc le même nœud, si elle ne diffèrent que par le croisement qu'on décide de numéroter en premier. C'est pourquoi deux couplages qui se déduisent l'un de l'autre par permutation circulaire doivent être considérés comme équivalents et comptés seulement une fois. Edgar Gilbert a résolu cette variante du problème d'énumération, en prouvant que le nombre de couplages à équivalence près est (en fonction du nombre de croisements n = 3, 4, 5, …) :

1, 2, 5, … (suite A002484 de l'OEIS).

Notes et références

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Ménage problem » (voir la liste des auteurs).
• (en) Nguyen-Huu Bong, « Lucas numbers and the menage problem », International Journal of Mathematical Education in Science and Technology, vol. 29, n^o 5,‎ 1998, p. 647–661 (DOI 10.1080/0020739980290502)
• (en) Heinrich Dörrie (trad. David Antin), 100 Great Problems of Elementary Mathematics, Dover, 1965, 393 p. (ISBN 978-0-486-61348-2, lire en ligne), chap. VIII (« Lucas' Problem of the Married Couples »), p. 27–33
• (en) Lars Holst, « On the “problème des ménages” from a probabilistic viewpoint », Statistics and Probability Letters, vol. 11, n^o 3,‎ 1991, p. 225–231 (DOI 10.1016/0167-7152(91)90147-J)
• (en) Irving Kaplansky, « Solution of the problème des ménages », Bull. Amer. Math. Soc., vol. 49, n^o 10,‎ 1943, p. 784–785 (DOI 10.1090/S0002-9904-1943-08035-4, lire en ligne, consulté le 25 décembre 2010)
• (en) Irving Kaplansky et John RiordanJohn Riordan (mathématicien), « The problème des ménages », Scripta Mathematica, vol. 12,‎ 1946, p. 113–124
• (en) John Riordan, « The arithmetic of ménage numbers », Duke Mathematical Journal, vol. 19,‎ 1952, p. 27–30 (DOI 10.1215/S0012-7094-52-01904-2)
• (en) Lajos Takács, « On the “problème des ménages” », Discrete Mathematics, vol. 36, n^o 3,‎ 1981, p. 289–297 (DOI 10.1016/S0012-365X(81)80024-6)

Liens externes

• (en) Eric W. Weisstein, « Married Couples Problem », sur MathWorld
• (en) Eric W. Weisstein, « Laisant's Recurrence Formula », sur MathWorld